前回のStanford University/CS131/宿題6-1 Image Compression(画像圧縮)とFace Dataset(顔データセット)の続きをやる。今回の宿題は、k-Nearest Neighbor(K近傍法)とCross-Validation(交差検証)をカバーする。
Part 2 – k-Nearest Neighbor¶
We’re now going to try to classify the test images using the k-nearest neighbors algorithm on the raw features of the images (i.e. the pixel values themselves). We will see later how we can use kNN on better features.
次に、raw features of the imagesのk近傍法アルゴリズムを使用してテスト画像の分類を試みる(画素が自身を評価するみたいな)。後半で、もっとましな特徴に対してどうKNNを利用できるか見ていく。
Here are the steps that we will follow:
以下に今後の手順を示す。
-
We compute the L2 distances between every element of X_test and every element of X_train in compute_distances.
compute_distancesで、X_testとX_trainの全要素間のL2距離を計算する。 -
We split the dataset into 5 folds for cross-validation in split_folds.
split_foldsにおいて、交差検証用にデータセットを5分割する。 -
For each fold, and for different values of $k$, we predict the labels and measure accuracy.
各分割に対して、そして、異なる$k$の値に対してラベルを予測して正確度を測る。 -
Using the best $k$ found through cross-validation, we measure accuracy on the test set.
交差検証によって見つけたベスト$k$を用いて、テストセットを使用して精度を評価する。
from time import time
from collections import defaultdict
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rc
from skimage import io
from utils import load_dataset
%matplotlib inline
plt.rcParams['figure.figsize'] = (15.0, 10.0) # set default size of plots
plt.rcParams["font.size"] = "17"
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
def compute_distances(X1, X2):
"""Compute the L2 distance between each point in X1 and each point in X2.
It's possible to vectorize the computation entirely (i.e. not use any loop).
Args:
X1: numpy array of shape (M, D) normalized along axis=1
X2: numpy array of shape (N, D) normalized along axis=1
Returns:
dists: numpy array of shape (M, N) containing the L2 distances.
"""
M = X1.shape[0]
N = X2.shape[0]
assert X1.shape[1] == X2.shape[1]
dists = np.zeros((M, N))
# YOUR CODE HERE
# Compute the L2 distance between all X1 features and X2 features.
# Don't use any for loop, and store the result in dists.
#
# You should implement this function using only basic array operations;
# in particular you should not use functions from scipy.
#
# HINT: Try to formulate the l2 distance using matrix multiplication
a = np.sum(X1**2,axis=1).reshape((M,1))
b = np.sum(X2**2,axis=1).reshape((1,N))
ab = X1.dot(X2.T)
dists = np.sqrt(a-2*ab+b)
#dists = np.linalg.norm(M-N)
# END YOUR CODE
assert dists.shape == (M, N), "dists should have shape (M, N), got %s" % dists.shape
return dists
X_train, y_train, classes_train = load_dataset('faces', train=True, as_gray=True)
X_test, y_test, classes_test = load_dataset('faces', train=False, as_gray=True)
assert classes_train == classes_test
classes = classes_train
# Flatten the image data into rows
# we now have one 4096 dimensional featue vector for each example
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
# Step 1: compute the distances between all features from X_train and from X_test
dists = compute_distances(X_test, X_train)
assert dists.shape == (160, 800)
print("dists shape:", dists.shape)
def predict_labels(dists, y_train, k=1):
"""Given a matrix of distances `dists` between test points and training points,
predict a label for each test point based on the `k` nearest neighbors.
Args:
dists: A numpy array of shape (num_test, num_train) where dists[i, j] gives
the distance betwen the ith test point and the jth training point.
Returns:
y_pred: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
num_test, num_train = dists.shape
y_pred = np.zeros(num_test, dtype=np.int)
for i in range(num_test):
# A list of length k storing the labels of the k nearest neighbors to
# the ith test point.
closest_y = []
# Use the distance matrix to find the k nearest neighbors of the ith
# testing point, and use self.y_train to find the labels of these
# neighbors. Store these labels in closest_y.
# Hint: Look up the function numpy.argsort.
# Now that you have found the labels of the k nearest neighbors, you
# need to find the most common label in the list closest_y of labels.
# Store this label in y_pred[i]. Break ties by choosing the smaller
# label.
# YOUR CODE HERE
idx = np.argsort(dists[i,:])
for j in range(k):
closest_y.append(y_train[idx[j]])
y_pred[i] = max(set(closest_y),key=closest_y.count)
# END YOUR CODE
return y_pred
# We use k = 1 (which corresponds to only taking the nearest neighbor to decide)
y_test_pred = predict_labels(dists, y_train, k=1)
# Compute and print the fraction of correctly predicted examples
num_test = y_test.shape[0]
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
Cross-Validation¶
We don’t know the best value for our parameter $k$.
There is no theory on how to choose an optimal $k$, and the way to choose it is through cross-validation.
パラメータ$k$の最良値は未知である。$k$の最適値を選択するための理論は存在せず、$k$最適値選択法は交差検証を介してである。
We cannot compute any metric on the test set to choose the best $k$, because we want our final test accuracy to reflect a real use case. This real use case would be a setting where we have new examples come and we classify them on the go. There is no way to check the accuracy beforehand on that set of test examples to determine $k$.
テストセットにおいては、$k$の最適値を選択する目的でメトリックを算出することは不可能だ。何故なら、最終的なテスト精度は実用に耐えうる必要があるからだ。ここで言う実用とは、新しい標本を得てそれらをその場で分類するということだ。$k$を判別するために事前にそのテスト標本セットを使って精度を確認する方法は存在しない。
Cross-validation will make use split the data into different fold (5 here).
For each fold, if we have a total of 5 folds we will have:
交差検証は、データを異なる層(ここでは5)に分割する。各層に関して、合計5層の場合
- 80% of the data as training data
データの80%が訓練データ - 20% of the data as validation data
データの20%が検証データ
We will compute the accuracy on the validation accuracy for each fold, and use the mean of these 5 accuracies to determine the best parameter $k$.
各層に対する検証精度の正確度を算出し、これら5つの正確度の平均を使用して最適パラメータ$k$を決定する。
def split_folds(X_train, y_train, num_folds):
"""Split up the training data into `num_folds` folds.
The goal of the functions is to return training sets (features and labels) along with
corresponding validation sets. In each fold, the validation set will represent (1/num_folds)
of the data while the training set represent (num_folds-1)/num_folds.
If num_folds=5, this corresponds to a 80% / 20% split.
For instance, if X_train = [0, 1, 2, 3, 4, 5], and we want three folds, the output will be:
X_trains = [[2, 3, 4, 5],
[0, 1, 4, 5],
[0, 1, 2, 3]]
X_vals = [[0, 1],
[2, 3],
[4, 5]]
Args:
X_train: numpy array of shape (N, D) containing N examples with D features each
y_train: numpy array of shape (N,) containing the label of each example
num_folds: number of folds to split the data into
jeturns:
X_trains: numpy array of shape (num_folds, train_size * (num_folds-1) / num_folds, D)
y_trains: numpy array of shape (num_folds, train_size * (num_folds-1) / num_folds)
X_vals: numpy array of shape (num_folds, train_size / num_folds, D)
y_vals: numpy array of shape (num_folds, train_size / num_folds)
"""
assert X_train.shape[0] == y_train.shape[0]
validation_size = X_train.shape[0] // num_folds
training_size = X_train.shape[0] - validation_size
X_trains = np.zeros((num_folds, training_size, X_train.shape[1]))
y_trains = np.zeros((num_folds, training_size), dtype=np.int)
X_vals = np.zeros((num_folds, validation_size, X_train.shape[1]))
y_vals = np.zeros((num_folds, validation_size), dtype=np.int)
# YOUR CODE HERE
# Hint: You can use the numpy array_split function.
X_lst = np.array_split(X_train,num_folds,axis=0)
y_train = y_train.reshape(-1, 1)
y_lst = np.array_split(y_train,num_folds,axis=0)
for i in range(num_folds):
X_vals[i,:,:] = X_lst[i]
X_trains[i,:,:] = np.vstack(X_lst[:i]+X_lst[i+1:])
y_vals[i,:] = y_lst[i][:,0]
y_trains[i,:] = np.vstack(y_lst[:i]+y_lst[i+1:])[:,0]
# END YOUR CODE
return X_trains, y_trains, X_vals, y_vals
# Step 2: split the data into 5 folds to perform cross-validation.
num_folds = 5
X_trains, y_trains, X_vals, y_vals = split_folds(X_train, y_train, num_folds)
assert X_trains.shape == (5, 640, 4096)
assert y_trains.shape == (5, 640)
assert X_vals.shape == (5, 160, 4096)
assert y_vals.shape == (5, 160)
# Step 3: Measure the mean accuracy for each value of `k`
# List of k to choose from
k_choices = list(range(5, 101, 5))
# Dictionnary mapping k values to accuracies
# For each k value, we will have `num_folds` accuracies to compute
# k_to_accuracies1 will be for instance [0.22, 0.23, 0.19, 0.25, 0.20] for 5 folds
k_to_accuracies = {}
for k in k_choices:
print("Running for k=%d" % k)
accuracies = []
for i in range(num_folds):
# Make predictions
fold_dists = compute_distances(X_vals[i], X_trains[i])
y_pred = predict_labels(fold_dists, y_trains[i], k)
# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_pred == y_vals[i])
accuracy = float(num_correct) / len(y_vals[i])
accuracies.append(accuracy)
k_to_accuracies[k] = accuracies
# plot the raw observations
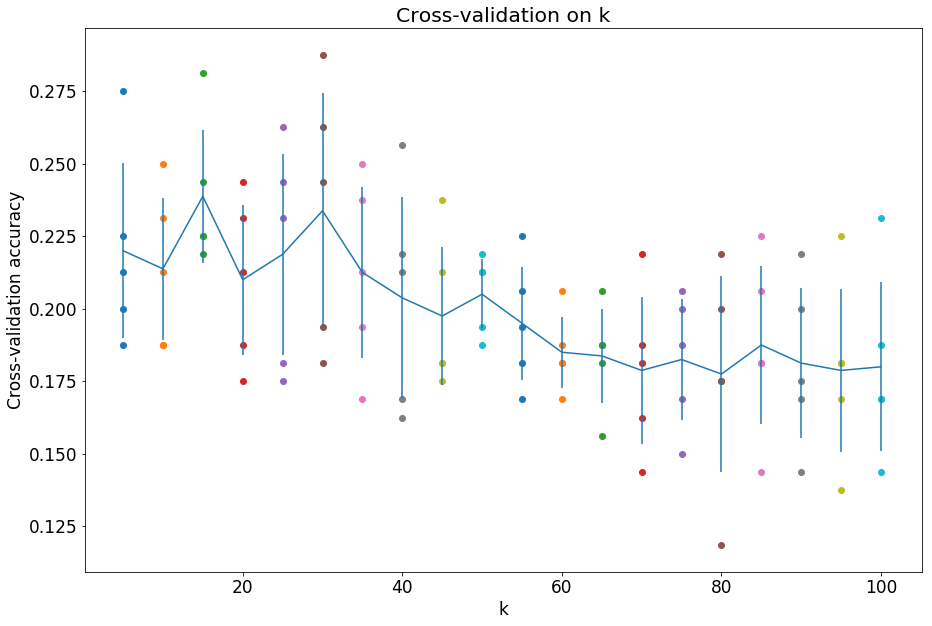
for k in k_choices:
accuracies = k_to_accuracies[k]
plt.scatter([k] * len(accuracies), accuracies)
# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()
# Based on the cross-validation results above, choose the best value for k,
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 26% accuracy on the test data.
best_k = None
# YOUR CODE HERE
# Choose the best k based on the cross validation above
best_k = 2
# END YOUR CODE
y_test_pred = predict_labels(dists, y_train, k=best_k)
# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('For k = %d, got %d / %d correct => accuracy: %f' % (best_k, num_correct, num_test, accuracy))