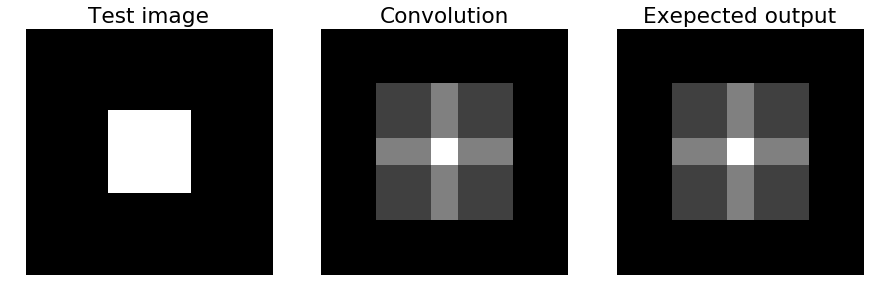Stanford University/CS131/Homework1をやる。Homework0に比べるとはるかにハイレベルなのでいきなりやる気が無くなるが、無理のないように1日少しずつやっていこうと思う。そもそも1セメスターは4ヶ月あるので、4ヶ月がかりでやればいいわけである。

Part 1: Convolutions¶

Commutative Property¶

Recall that the convolution of an image $f:\mathbb{R}^2\rightarrow \mathbb{R}$ and a kernel $h:\mathbb{R}^2\rightarrow\mathbb{R}$ is defined as follows:
$$(f*h)[m,n]=\sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty f[i,j]\cdot h[m-i,n-j]$$

Or equivalently,
\begin{align}
(f*h)[m,n] &= \sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty h[i,j]\cdot f[m-i,n-j]\\
&= (h*f)[m,n] \end{align}

Show that this is true (i.e. prove that the convolution operator is commutative: $f*h = h*f$).

畳み込み演算子が可換性$f*h = h*f$であることを証明する。
\begin{align}
(f*h)[m,n] &= \sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty f[i,j]\cdot h[m-i,n-j]\\
&= \sum_{x=\infty}^{-\infty}\sum_{y=\infty}^{-\infty} f[m-x,n-y]\cdot h[x,y]\\
&= \sum_{x=-\infty}^\infty\sum_{y=-\infty}^\infty f[m-x,n-y]\cdot h[x,y]\\
&= \sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty h[i,j]\cdot f[m-i,n-j]\\
&= (h*f)[m,n] \end{align}

Linear and Shift Invariance (10 points)¶

Let $f$ be a function $\mathbb{R}^2\rightarrow\mathbb{R}$. Consider a system $f\xrightarrow{s}g$, where $g=(f*h)$ with some kernel $h:\mathbb{R}^2\rightarrow\mathbb{R}$. Show that $S$ defined by any kernel $h$ is a Linear Shift Invariant (LSI) system. In other words, for any $h$, show that $S$ satisfies both of the following:

$S[a\cdot{f_1}+b\cdot{f_2}]= a\cdot{S[f_1]}+b\cdot{S[f_2]}$
If $f[m,n]\xrightarrow{s}g[m,n]$ then $f[m-m_0,n-n_0]\xrightarrow{s}g[m-m_0,n-n_0]$

全てのカーネル$h$によって定義付けられる$S$が線形シフト不変システムであることを証明する。言い換えると、全ての$h$に対して$S$が上記の両方を満たすことを証明する。

\begin{align}
S[a\cdot{f_1}+b\cdot{f_2}] &= (a\cdot{f_1}+b\cdot{f_2})*h\\
&= a\cdot({f_1}*h)+b\cdot({f_2}*h)\\
&= a\cdot{S[{f_1}]}+b\cdot{S[{f_2}]}\\
\end{align}
\begin{align}
f[m-m_0,n-n_0] &\xrightarrow{s} \sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty f[i,j]\cdot h[m-m_0-i,n-n_0-j]\\
&= g[m-m_0,n-n_0] \end{align}

Implementation¶

In this section, you will implement two versions of convolution:
このセクションでは、下記の2バージョンの畳み込みを実装する。

conv_nested
conv_fast

First, run the code cell below to load the image to work with.
先ず、下のセルを実行して作業用の画像をロードする。

# Setup
import numpy as np
import matplotlib.pyplot as plt
from time import time
from skimage import io

from __future__ import print_function

%matplotlib inline
plt.rcParams['figure.figsize'] = 15.0, 10.0 # set default size of plots
plt.rcParams["font.size"] = "18"
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

# for auto-reloading extenrnal modules
%load_ext autoreload
%autoreload 2

The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload

# Open image as grayscale
img = io.imread('dog.jpg', as_grey=True)

# Show image
plt.imshow(img)
plt.axis('off')
plt.title("Isn't he cute?")
plt.show()

/root/.pyenv/versions/3.7.0/envs/py37/lib/python3.7/site-packages/skimage/io/_io.py:49: UserWarning: `as_grey` has been deprecated in favor of `as_gray`
  warn('`as_grey` has been deprecated in favor of `as_gray`')

Now, implement the function conv_nested in filters.py. This is a naive implementation of convolution which uses 4 nested for-loops. It takes an image $f$ and a kernel $h$ as inputs and outputs the convolved image $(f*h)$ that has the same shape as the input image. This implementation should take a few seconds to run.
次に、filters.pyにconv_nested関数を実装する。これは、4個のネスト化for-loopsを使用している単純な畳み込み実装だ。この実装は、入力に画像$f$とカーネル$h$を受け取って、入力画像と同じ形の畳み込み画像を出力する。この実装は実行に数秒を要する。

Hint: It may be easier to implement $(h*f)$
Hint: $(h*f)$を実装するのが簡単かもしれない。

We’ll first test your conv_nested function on a simple input.
最初に簡単な入力を用いて実装したconv_nested関数をテストする。

def conv_nested(image, kernel):
    """A naive implementation of convolution filter.
    This is a naive implementation of convolution using 4 nested for-loops.
    This function computes convolution of an image with a kernel and outputs
    the result that has the same shape as the input image.
    Args:
        image: numpy array of shape (Hi, Wi)
        kernel: numpy array of shape (Hk, Wk)
    Returns:
        out: numpy array of shape (Hi, Wi)
    """
    Hi, Wi = image.shape
    Hk, Wk = kernel.shape
    out = np.zeros((Hi, Wi))
    ### YOUR CODE HERE
    # for-loopsを4個作る
    for m in range(Hi-1): # hight(高さ)※-1がないとエラー
        for n in range(Wi-1): # width(横幅)※-1がないとエラー
            for i in range(Hk): # Hkernel(Kernel高さ)
                for j in range(Wk): # Wkernel(kernel幅)
                    # image=f, kernel=h ※+1がないとエラー
                    out[m,n]+=image[m+1-i][n+1-j]*kernel[i,j]
    ### END YOUR CODE
    return out

# Simple convolution kernel.
kernel = np.array(
[
    [1,0,1],
    [0,0,0],
    [1,0,1]
])

# Create a test image: a white square in the middle
test_img = np.zeros((9, 9))
test_img[3:6, 3:6] = 1

# Run your conv_nested function on the test image
test_output = conv_nested(test_img, kernel)

# Build the expected output
expected_output = np.zeros((9, 9))
expected_output[2:7, 2:7] = 1
expected_output[4, 2:7] = 2
expected_output[2:7, 4] = 2
expected_output[4, 4] = 4

# Plot the test image
plt.subplot(1,3,1)
plt.imshow(test_img)
plt.title('Test image')
plt.axis('off')

# Plot your convolved image
plt.subplot(1,3,2)
plt.imshow(test_output)
plt.title('Convolution')
plt.axis('off')

# Plot the exepected output
plt.subplot(1,3,3)
plt.imshow(expected_output)
plt.title('Exepected output')
plt.axis('off')
plt.show()

# Test if the output matches expected output
assert np.max(test_output - expected_output) < 1e-10, "Your solution is not correct."

Now let’s test your conv_nested function on a real image.
今度は実画像でconv_nested関数をテストする。

import time
# Simple convolution kernel.
# Feel free to change the kernel and to see different outputs.
kernel = np.array(
[
    [1,0,-1],
    [2,0,-2],
    [1,0,-1]
])
start = time.time()
out = conv_nested(img, kernel)
end = time.time()
print(end - start)
# Plot original image
plt.subplot(2,2,1)
plt.imshow(img)
plt.title('Original')
plt.axis('off')

# Plot your convolved image
plt.subplot(2,2,3)
plt.imshow(out)
plt.title('Convolution')
plt.axis('off')

# Plot what you should get
solution_img = io.imread('convoluted_dog.jpg', as_gray=True)
plt.subplot(2,2,4)
plt.imshow(solution_img)
plt.title('What you should get')
plt.axis('off')
plt.show()

0.7278103828430176

この問題を解くだけでかなりの時間を要したので、今日はこのぐらいにしておくが、これを大学一年で履修するのはかなり厳しそうだ。A survivor’s guide to Artificial Intelligence courses at Stanfordによると、CS131はSophomore(大学2年)のfall semester(秋学期で大学2年の1学期)で履修するのがいいようだ。あるいは、大学一年のサマースクールで履修するのも有りかもしれない。まぁ、サマースクールまで取ると、学費がとんでもない額になりそうなので、スタンフォード大学留学はよほどの金持ちか、大学からfull scholarship(全額支給奨学金)を受けられる超優秀な学生以外は無理だろう。